Clases de sistemas de numeracion

 EL SISTEMA EGIPCIO Los antiguos egipcios, que vivían en el valle del Nilo, alcanzaron un alto nivel de civilización antes del año 3000 a.de C.  Entre sus logros estaba la escritura llamada jeroglífica y un sistema de numeración que era puramente decimal (de base diez) cuyos símbolos aparecen en la tabla.  
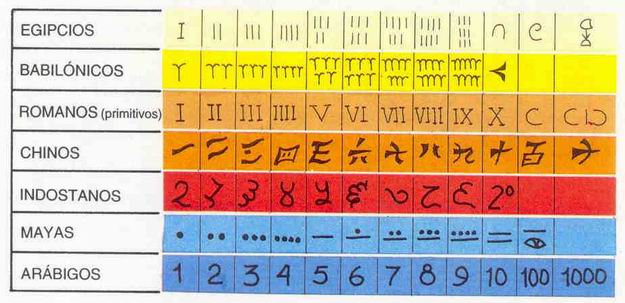
Cada símbolo podía repetirse hasta nueve veces y el número representado se encontraba sumando los valores de cada uno de los símbolos utilizados.



 4.3 EL SISTEMA ROMANO Es fácil entender los números romanos.  Este sistema numérico usa 7 letras mayúsculas que  significan:  
I 1 V 5 X 10 L 50 C 100 D 500 M 1000
4.3.1

 Recordemos las reglas: Los símbolos  I, X, C, M  no se pueden repetir más de tres veces seguidas. Se suman a la derecha de un símbolo igual o mayor y se restan a la izquierda de uno mayor. El símbolo I solo puede anteponerse a V y X,  y el símbolo  X solo puede anteponerse a L y C. Los símbolos V, L, D y M no se restan. Una raya sobre uno a más símbolos indica que se debe multiplicar por mil el valor que ellos representan. El valor de los números romanos queda multiplicado por mil tantas veces como guiones haya en su parte superior

Ejemplos de sistemas de numeracion

Imagenes sobre el sistema de numeracion

Videos de sistema de numeracion

Sistema de numeracion

1 ¿QUÉ ES UN SISTEMA DE NUMERACIÓN?

  Cualquier sistema consta fundamentalmente de una serie de elementos que lo conforman, una serie de reglas que permite establecer operaciones y relaciones entre tales elementos. Por ello, puede decirse que un sistema de numeración es el conjunto de elementos (símbolos o números), operaciones y relaciones que por intermedio de reglas propias, permite establecer el papel de tales relaciones y operaciones. Historia
Los hombres supieron asociar tempranamente a una colección de objetos un grupo de signos o de cosas: trazos marcados en la madera, en un hueso o en la arena, montones de piedras, gestos con la mano o con la cabeza, etc. Así, los pastores sumerios llevaban la cuenta de los nacimientos, pérdidas, compras y ventas de sus ovejas representando cada animal del rebaño mediante un cono.
de arcilla (calculi) colocado en una envoltura de arcilla. La economía, más compleja, de las primeras aglomeraciones urbanas de la Baja Mesopotamia eligió un sistema más elaborado: se imprimieron sobre la envoltura de arcilla signos que representaban los mismos signos que los calculi.   Estos últimos, que ya no tenían razón de ser, fueron poco a poco suprimidos, y las envolturas reemplazadas por las primeras tablillas, numerales. Por tanto, las primeras numeraciones escritas aparecieron al mismo tiempo que las primeras formas de escritura, en Mesopotamia hacia 3300 a. J. C. y en Egipto hacia 3200 a. J. C.

REPRESENTACIÓN DE NÚMEROS: Mucho antes de inventar la escritura, el hombre empezó a rayar las losas y paredes de las cuevas y a tallar muescas en varas para indicar “cuantos”.  Tales marcas fueron el inicio de los sistemas de numeración.

Videos sobre conjuntos

imagenes sobre conjuntos

Links sobre los conjuntos

Ejemplos de conjuntos

Definición de Conjunto

CONJUNTOS

DATO HISTÓRICO: En la historia de las matemáticas, la teoría de conjuntos surge como resultado de las investigaciones acerca de los números y sus propiedades.  Los inicios de la teoría de conjuntos se asocian con Jorge Cantor (1845 – 1918) quien sentó las bases para su desarrollo como teoría matemática de importancia fundamental.  Después de Cantor la teoría de conjuntos alcanzó su fundamentación definitiva.  Muchos de los temas de la teoría de conjuntos pueden ser identificados en las matemáticas griegas, pero se incorporan al cuerpo organizado del saber matemático en los finales del siglo XIX y los principios del siglo XX.    Leamos ahora el concepto primitivo de conjunto: Toda colección de objetos es un conjunto y cada objeto de la colección recibe el nombre de elemento del conjunto.

Leamos otros conceptos:
La palabra conjunto se refiere a un concepto fundamental que no se define en matemáticas se trata de una colección de seres u objetos.
Es una agrupación cualquiera de objetos con una característica específica que permite determinar con certeza si un objeto pertenece o no pertenece a la agrupación.

videos sobre el tema de preposiciones

imagen de proposiciones

Links a paginas sobre preposiciones

3.1.1 Concepto de Proposición. | LÓGICA MATEMÁTICA

Ejemplo de Proposiciones

LAS PROPOSICIONES

Una proposición o enunciado es una oración que puede ser falso o verdadero pero no ambas a la vez. La proposición es un elemento fundamental de la lógica matemática. A continuación se tienen algunos ejemplos de proposiciones válidas y no válidas, y se explica porqué algunos enunciados no son proposiciones. Las proposiciones se indican por medio de una letra minúscula, dos puntos y la proposición propiamente dicha.

Ejemplo.:
 La tierra es plana.
  q: 17 - 8 = 9
  r: x > y-9
  s: El Cúcuta será campeón en el primer semestre del 2016
 t: Hola
¿cómo estás?
 w:  Lava el carro, por favor.